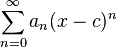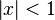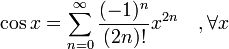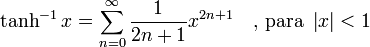jueves, 26 de mayo de 2011
4.3 Serie de potencias.
Series de potencias
Una serie de potencias alrededor de x=0 es una serie de la forma:
http://www.mitecnologico.com/Main/SeriesDePotencia
Series De Potencia Series de potencias Convergencia de las series de potencias Definición Recibe el nombre de serie de potencias toda serie de la forma ∞Σ n=0 an(x−c)n. El número real an se denomina coeficiente n-ésimo de la serie de potencias (obsérvese que el término n-ésimo de la serie es an(x−c)n). Si los coeficientes a0, a1, am−1 son nulos, la serie suele escribirse ∞Σ n=m an(x−c)n. En cierto modo, se trata de una especie de polinomio con infinitos términos. Vamos a ver que las funciones definidas como suma de una serie de potencias comparten muchas propiedades con los polinomios. ¿Para qué valores de x converge una serie de potencias? Obviamente, es segura la convergencia para x =c, con suma a0, y puede suceder que éste sea el único punto en el que la serie converge. Fuera de este caso extremo, la situación es bastante satisfactoria: veamos algunos ejemplos. Ejemplos. a) La serie geométrica ∞Σ n=0 xn converge (absolutamente) si y solo si x “ (−1,1) (con suma 11−x , como sabemos). 189
Una serie de potencias alrededor de x=c es una serie de la forma:
En el cual el centro es c, y los coeficientes an son los términos de una sucesion.
[editar] Ejemplos
- La serie geométrica
 es una serie de potencias absolutamente convergente si | x | < 1 y divergente si | x | > 1 ó | x | = 1
es una serie de potencias absolutamente convergente si | x | < 1 y divergente si | x | > 1 ó | x | = 1
- La serie de potencias
 es absolutamente convergente para todo
es absolutamente convergente para todo 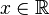
- La serie de potencias
 solamente converge para x = 0
solamente converge para x = 0
http://www.mitecnologico.com/Main/SeriesDePotencia
4.4 Radio de convergencia.
Radio de convergencia
En matemáticas, según el teorema de Cauchy-Hadamard, el radio de convergencia de una serie de la forma  , con
, con  , viene dado por la expresión:
, viene dado por la expresión:
 , con
, con  , recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r, x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0. Si lo hace para cualquier valor de x, r =
, recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r, x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0. Si lo hace para cualquier valor de x, r = 
 .
.
(para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es r = 1. Eso significa que para calcular si tomo cualquier valor cuya distancia al x0 = 0 es menor que r = 1, por ejemplo el x = 0.25, entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho
 .
.
(la cuenta se puede hacer por serie de potencia). Y por otro lado
 .
.
Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el x = 2, los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia). Efectivamente:
 .
.
 .
.
Pero en este caso su radio de convergencia es r = 2. Notemos que la función 1 / (1 − x) tiene una singularidad en el 1; y que en los dos caso anteriores el radio de convergencia coincide con la distancia del centro a la singularidad: | 0 − 1 | = 1 y | 3 − 1 | = 2. Esto será siempre verdadero para ésta función, pero, no puede generalizarse, como veremos en el siguiente ejemplo:
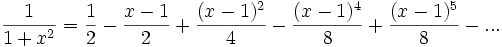
Como no hay singularidades reales podría suponerse que el radio es infinito, sin embargo su radio de convergencia es . Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador.La serie
. Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador.La serie
 .
.
y esto vale para todo real x por eso el radio de convergencia será infinito.
informacion obtenida de http://es.wikipedia.org/wiki/Radio_de_convergencia
 , con
, con  , viene dado por la expresión:
, viene dado por la expresión:Definición
Si nos limitamos al conjunto de los números reales, una serie de la forma , con
, con  , recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r, x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0. Si lo hace para cualquier valor de x, r =
, recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r, x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0. Si lo hace para cualquier valor de x, r = 
Ejemplos
Mostraremos el radio de convergencia de algunos desarrollos en series de potencias con sus respectivos radios de convergencia sin justificar porqué el radio de convergencia es el dado.Radio de convergencia finito
La función 1 / (1 − x) en su desarrollo con centro 0, o sea, en series de potencia x − x0 = x − 0 = x, tiene el siguiente aspecto: .
.(para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es r = 1. Eso significa que para calcular si tomo cualquier valor cuya distancia al x0 = 0 es menor que r = 1, por ejemplo el x = 0.25, entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho
 .
.(la cuenta se puede hacer por serie de potencia). Y por otro lado
 .
.Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el x = 2, los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia). Efectivamente:
 .
.Distancia a la singularidad
El cálculo del radio de convergencia no es simple. Veamos una función con dos desarrollos en serie con distintos centros y analicemos sus radios de convergencia. La misma función 1 / (1 − x) en su desarrollo con centro x0 = 3 tiene la forma: .
.Pero en este caso su radio de convergencia es r = 2. Notemos que la función 1 / (1 − x) tiene una singularidad en el 1; y que en los dos caso anteriores el radio de convergencia coincide con la distancia del centro a la singularidad: | 0 − 1 | = 1 y | 3 − 1 | = 2. Esto será siempre verdadero para ésta función, pero, no puede generalizarse, como veremos en el siguiente ejemplo:
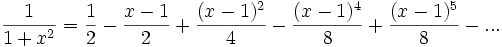
Como no hay singularidades reales podría suponerse que el radio es infinito, sin embargo su radio de convergencia es
 . Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador.La serie
. Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador.La serieRadio de convergencia infinito
Por ejempo, la función ex puede desarrollarse en series de potencia de x − 0 = x, de hecho .
.y esto vale para todo real x por eso el radio de convergencia será infinito.
informacion obtenida de http://es.wikipedia.org/wiki/Radio_de_convergencia
miércoles, 25 de mayo de 2011
4.5 Serie de Taylor.
- SERIE DE TAYLOR En matemáticas, la serie de Taylor de una función f(x) infinitamente derivable (real o compleja) definida en un intervalo abierto ( a - r , a + r ) se define como la siguiente suma: Aquí, n ! es el factorial de n y f ( n ) ( a ) indica la n-ésima derivada de f en el punto a .
- Si esta serie converge para todo x perteneciente al intervalo ( a - r , a + r ) y la suma es igual a f ( x ), entonces la función f ( x ) se llama analítica . Para comprobar si la serie converge a f ( x ), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor. Si a = 0, a la serie se le llama serie de Maclaurin .
- Esta representación tiene tres ventajas importantes:
- La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.
- Se puede utilizar para calcular valores aproximados de la función.
- Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.
- Una aproximación de octavo orden de la función coseno en el plano de los complejos.
- EJEMPLO Usando los términos de la serie de Taylor centrada en cero, aproxime la función f(x)=SEN X con base en el valor de la función f y sus derivadas en el punto x=0,5. Empiece con solo el termino n=0 agregando sucesivamente un término hasta el error porcentual sea menor que la tolerancia, tomando 3 cifras significativas.
- EJEMPLO Remplazando la función tenemos: Sen X= sen (0)+cos(o)x - sen (0) X^2/2! - cos (o) X^3 /3! + sen(0) X^4/4! Entonces, Sen X= X – X^3/3! - X^5/5! …… Ahora remplazamos termino por termino para ver el error y de esta forma llegar a la tolerancia permitida Sen X 1 = 0.5 Sen X 2 = 0.479 Sen X 3 = 0.478
- EJEMPLO Con el tercer termino cumplimos con la tolerancia exigida.
- EJEMPLO Con el tercer termino cumplimos con la tolerancia exigida.
4.6 Representación de funciones mediante la serie de Taylor.
A continuación se enumeran algunas series de Taylor de funciones básicas. Todos los desarrollos son también válidos para valores complejos de x.
 complejo
complejo


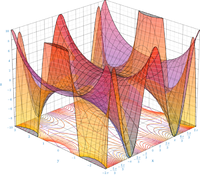
Serie geométrica
Teorema del binomio
y cualquierpara
 complejo
complejoFunciones trigonométricas
-
- Donde Bs son los Números de Bernoulli.
Funciones hiperbólicas
Función W de Lambert



jueves, 19 de mayo de 2011
4.7 Calculo de Integrales de funciones expresadas como Serie de Taylor
La función p(x)=a0+a1x+a2x2+..........+anxn, en la que los coeficientes ak son constantes, se llama polinomio de grado n. En particular y=ax+b es un polinomio de primer grado e y=ax2+bx+c es un polinomio de segundo grado. Los polinomios pueden considerarse las funciones más sencillas de todas. Para calcular su valor para una x dada, necesitamos emplear únicamente las operaciones de adición, sustracción y multiplicación; ni siquiera la división es necesaria. Los polinomios son funciones continuas para todo x y tienen derivadas de cualquier orden. Además la derivada de un polinomio es también un polinomio de grado inferior en una unidad, y las derivadas de orden n+1 y superiores de un polinomio de grado n son nulas.
Si a los polinomios añadimos las funciones de la forma y=p(x)/q(x) (cociente de polinomios, para cuyo cálculo necesitamos también de la división), las funciones raíz cuadrada de x y raíz cúbica de x, y finalmente, las combinaciones aritméticas de los tipos anteriores, obtenemos esencialmente las funciones cuyos valores pueden calcularse por métodos aprendidos en el bachillerato.
A este nivel se tienen nociones de algunas otras funciones tales como log(x), sen(x), ex, ..., pero, aunque se estudian sus propiedades más importantes, no se da una respuesta a las preguntas: ¿Cómo calcularlas? ¿Qué clase de operaciones, por ejemplo, es necesario realizar sobre la x para obtener log(x) o sen(x)?. La respuesta a estas preguntas la proporcionan los métodos desarrollados por el análisis matemático. Examinemos uno de estos métodos.
Fórmula de TaylorSea f(x) una función definida en un intervalo que contiene al punto a, con derivada de todos los órdenes.
El polinomio de primer grado p1(x) = f(a) + f ' (a) (x-a) tiene el mismo valor que f(x) en el punto x=a y también, como se comprueba fácilmente, la misma derivada que f(x) en este punto. Su gráfica es una recta tangente a la gráfica de f(x) en el punto a.
Es posible elegir un polinomio de segundo grado, p2(x) = f(a) + f ' (a) (x-a) + ½ f ' ' (a) (x-a)2, tal que en el punto x=a tenga el mismo valor que f(x) y valores también iguales para su primera y segunda derivadas. Su gráfica en el punto a se acercará a la de f(x) más que la anterior. Es natural esperar que si construimos un polinomio que en x=a tenga las mismas n primeras derivadas que f(x) en el mismo punto, este polinomio se aproximará más a f(x) en los puntos x próximos a a. Así obtenemos la siguiente igualdad aproximada, que es la fórmula de Taylor:f(x) ≈ f(a) + f '(a) (x-a) + (1/2!) f ' '(a) (x-a)2 + ...... + (1/n!) f (n)(a) (x-a) n
El segundo miembro de esta fórmula es un polinomio de grado n en (x-a). Para cada valor de x puede calcularse el valor de este polinomio si se conocen los valores de f(a) y de sus n primeras derivadas.
Para funciones que tienen derivada (n+1)-ésima, el segundo miembro de esta fórmula, como se demuestra fácilmente, difiere del primero en una pequeña cantidad que tiende a cero más rápidamente que (x-a)n. Además, es el único polinomio de grado n que difiere de f(x), para x próximo a a, en un valor que tiende a cero (cuando x tiende a a) más rápidamente que (x-a)n.
Si f(x) es un polinomio algebraico de grado n, entonces la igualdad aproximada anterior es una verdadera igualdad.
Si f(x) es un polinomio algebraico de grado n, entonces la igualdad aproximada anterior es una verdadera igualdad.
Para que sea exacta la igualdad aproximada anterior, debemos añadir al segundo miembro un término más, llamado resto:
f(x) = f(a)+f '(a)(x-a)+(1/2!) f ' '(a)(x-a)2+ ...... +(1/n!) f (n)(a)(x-a)n+(1/(n+1)!) f (n+1)(c)(x-a)n+1
El resto tiene la peculiaridad de que la derivada que en él aparece debe calcularse en cada caso, no en el punto a, sino en un punto c convenientemente elegido, desconocido, pero interior al intervalo de extremos a y x.
La demostración de la igualdad anterior es bastante engorrosa, aunque sencilla en esencia.Las leyes naturales pueden expresarse, por regla general, con buena aproximación por funciones derivables un número arbitrario de veces, y por ello pueden ser aproximadas por polinomios cuyo grado viene determinado por la precisión deseada.
La fórmula de Taylor, que abre el camino para la mayoría de los cálculos en el análisis aplicado, es muy importante desde el punto de vista práctico.
La idea de aproximar una función mediante polinomios o de representarla como suma de un número finito de funciones más sencillas alcanzó un gran desarrollo en el análisis, donde constituye ahora una rama independiente: la teoría de la aproximación de funciones
En las siguientes escenas podemos observar cómo la gráfica de las funciones se va "tapando" con la gráfica del polinomio de Taylor al aumentar el grado del polinomio. Para un valor de x calculamos la diferencia entre el valor real y el valor del polinomio correspondiente. Al aumentar el grado del polinomio esa diferencia es cada vez menor. Hemos calculado los polinomios de Taylor para a=0.
todo esta informacion fue sacada de:
Suscribirse a:
Entradas (Atom)